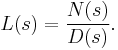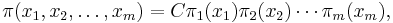BCMP network
In queueing theory, a discipline within the mathematical theory of probability, a BCMP network is a class of queueing network for which a product form equilibrium distribution exists. It is named after the authors of the paper where the network was first described: Baskett, Chandy, Muntz and Palacios. The theorem is a significant extension to a Jackson network allowing virtually arbitrary customer routing and service time distributions, subject to particular service disciplines.[1]
The paper is well known, and the theorem was described in 1990 as "one of the seminal achievements in queueing theory in the last 20 years" by J. Michael Harrison and Ruth Williams.[2]
Contents |
Definition of a BCMP network
A network of m interconnected queues is known as a BCMP network if each of the queues is of one of the following four types:
- FCFS discipline where all customers have the same negative exponential service time distribution. The service rate can be state dependent, so write
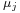 for the service rate when the queue length is j.
for the service rate when the queue length is j. - Processor sharing queues
- Infinite server queues
- LCFS with pre-emptive resume (work is not lost)
In the final three cases, service time distributions must have rational Laplace transforms. This means the Laplace transform must be of the form[3]
Also, the following conditions must be met.
- external arrivals to node i (if any) form a Poisson process,
- a customer completing service at queue i will either move to some new queue j with (fixed) probability
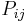 or leave the system with probability
or leave the system with probability 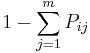 , which is non-zero for some subset of the queues.
, which is non-zero for some subset of the queues.
Theorem
For a BCMP network of m queues which is open, closed or mixed in which each queue is of type 1, 2, 3 or 4, the equilibrium state probabilities are given by
where C is a normalizing constant chosen to make the equilibrium state probabilities sum to 1 and 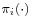 represents the equilibrium distribution for queue i.
represents the equilibrium distribution for queue i.
Proof
The theorem is proved by checking that the independent balance equations are satisfied.
Notes
- ^ Baskett, F.; Chandy, K. Mani; Muntz, R.R.; Palacios, F.G. (1975). "Open, closed and mixed networks of queues with different classes of customers". Journal of the ACM 22 (2): 248–260. doi:10.1145/321879.321887.
- ^ Harrison, J.M.; Williams, R.J. (1990). "On the Quasireversibility of a Multiclass Brownian Service Station". The Annals of Probability (Institute of Mathematical Statistics) 18 (3): 1249–1268. doi:10.1214/aop/1176990745. JSTOR 2244425.
- ^ Sinclair, Bart. "BCMP Theorem". Connexions. http://cnx.org/content/m10853/latest/. Retrieved 2011-08-14.